<!DOCTYPE html>
平行四边形专题复习一、平行四边形的基本性质
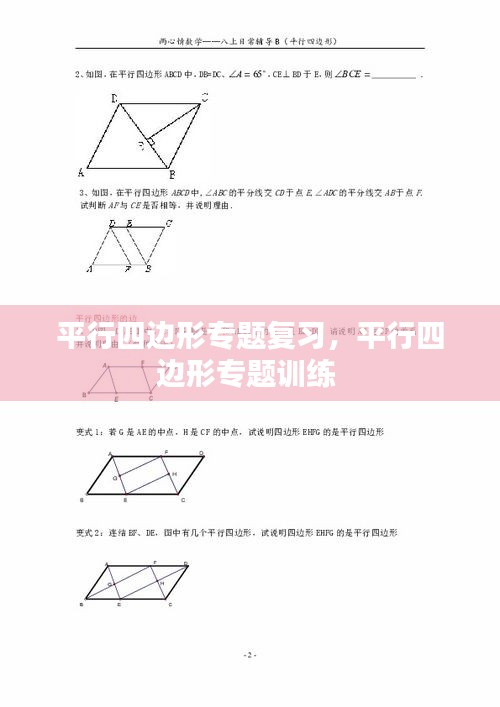
平行四边形是一种特殊的四边形,其对边两两平行。复习平行四边形的基本性质是理解其特征和进行相关计算的基础。以下是一些重要的性质:
1. 对边平行且相等:平行四边形的对边不仅平行,而且长度相等。
2. 对角相等:平行四边形的对角线互相平分,因此对角线所形成的四个角相等。
3. 对角线互相平分:平行四边形的两条对角线相交于它们的中点。
4. 相邻角互补:平行四边形的相邻角互补,即它们的和为180度。
5. 对角线所形成的三角形为等腰三角形:如果平行四边形的一条对角线不垂直于另一条对角线,那么它所形成的三角形是等腰三角形。
二、平行四边形的判定方法
在解决与平行四边形相关的问题时,正确判定一个四边形是否为平行四边形至关重要。以下是一些常用的判定方法:
1. 对边平行且相等:如果一个四边形的对边都平行且相等,则它是平行四边形。
2. 对角相等:如果一个四边形的对角相等,则它是平行四边形。
3. 对角线互相平分:如果一个四边形的对角线互相平分,则它是平行四边形。
4. 相邻角互补:如果一个四边形的相邻角互补,则它是平行四边形。
5. 有一组对边平行且相等的四边形是平行四边形:如果一个四边形有一组对边既平行又相等,则它是平行四边形。
三、平行四边形的计算应用
掌握平行四边形的计算方法是解决实际问题的重要工具。以下是一些常见的计算应用:
1. 计算平行四边形的面积:平行四边形的面积可以通过底乘以高来计算。
2. 计算对角线的长度:如果知道对角线的一半长度和夹角,可以使用余弦定理来计算对角线的长度。
3. 解平行四边形的几何问题:通过应用平行四边形的性质,可以解决一些几何问题,如找到未知角度或长度。
4. 解决实际问题:平行四边形的性质在建筑设计、城市规划等领域有广泛的应用。
四、典型例题解析
以下是一些典型的平行四边形例题,通过解析这些例题,可以帮助我们更好地理解和应用平行四边形的性质。
例题1:已知平行四边形ABCD,AB=10cm,BC=8cm,求AD的长度。
解析:由于ABCD是平行四边形,所以AB=CD,BC=AD。因此,AD的长度也是10cm。
例题2:已知平行四边形ABCD,对角线AC和BD相交于点O,且AC=8cm,BD=12cm,求AO和BO的长度。
解析:由于AC和BD互相平分,所以AO=OC=AC/2=4cm,BO=OD=BD/2=6cm。
五、总结与展望
平行四边形是几何学中的重要概念,掌握其基本性质和计算方法是学习几何的基础。通过对平行四边形的专题复习,我们可以更加深入地理解其特征和应用。在今后的学习中,我们应该注重以下方面:
1. 理解并熟练掌握平行四边形的性质。
2. 学会运用平行四边形的性质解决实际问题。
3. 不断积累典型例题,提高解题能力。
4. 将平行四边形的性质与其他几何知识相结合,形成完整的几何知识体系。
转载请注明来自牛查询星座网,本文标题:《平行四边形专题复习,平行四边形专题训练 》












 蜀ICP备2022005971号-1
蜀ICP备2022005971号-1
还没有评论,来说两句吧...